I know Shawn Cornally says you shouldn't call it SBG unless you go all the way with it, but I'm kinda getting my feet wet with it this year. One of the things I'm trying to implement is allowing students to re-quiz or re-test by request. I'm allowing them to just redo the sections that they missed. (I'm doing some other pieces of SBG including dividing their grades among various skills and giving more feedback that I have previously. But it's the re-quizzing that I want advice on here.)
So, we're two full weeks in as of tomorrow and I think students are already trying to take advantage of this situation. I should maybe give some background that may or may not also contribute to this:
I use a SMART board to write for my notes during class and there are a couple groups of students who think they can understand the material by spacing out during class and going home to download the notes then study right before the assessments. I don't mind if students have a hard time writing notes at the same time as listening to the material, so they can just sit back and pay attention and download the notes later. It's also useful for when students miss class for whatever reason to catch up. So, I don't want to quit using that option, but students don't seem to be "learning their lesson" very quickly.
I had one of those students come to class this afternoon (on quiz day) and say, "Mr. Petersen, I'm not going to do well on this quiz. In fact, you may not want to even grade it." So, I told him not to waste his time either and not even take it. This is all with the understanding that he would come in later to redo it. I can easily see this kid pushing it back further and further and, with the hope of bringing it up later, just failing the quarter and beyond.
Many other students, as I'm passing out the quiz, before they've even looked at it ask, "So, can we redo this quiz later?" I am glad that I can take some pressure off of them by saying that they can, but I get the feeling that they're just pushing back the responsibility and not taking the whole thing seriously.
If I were a college teacher, I'd just take the attitude of "your loss," but we can't really do that at public schools.
For any who have re-quizzing as part of your assessment system, is this always an issue? Any hints on what I can do to feel better about it?
Wednesday, August 25, 2010
Thursday, August 19, 2010
Math Puzzle Questions
Moments ago, @dandersod tweeted about an interesting, but non-intuitive probability problem. There are plenty in this genre such as the Monty Hall Problem and many in other areas like the uncountability of irrationals, area/perimeter relationships (@CmonMattTHINK), etc.
I think these problems are like lifting the wolverine's lip to show the teeth. Some kids will be like, "Wow! Those are sharp! So cool! I wonder what that wolverine would do to a rabbit..." Others will just be, "AHHH! Run away! Don't ever make me go near that thing ever again!"
These kinds of problems really separate those who end up loving math from those who do not. I present one or a dozen of these throughout the school year to my various math classes. Some of the kids LOVE it and try to figure out why it is and will read up on it when they go home and have all sorts of questions and really work to pay attention to the "proof." Others will just throw their hands up and say, "See! This is why I hate math!"
Basically, it polarizes the classroom. Those who enjoy thinking this way will get excited and encouraged to find out more. Those who already hate it will have fodder for their fears.
So, I guess what I'm asking here is: Is it a good idea to put forth these "paradoxical" problems in class?
I think these problems are like lifting the wolverine's lip to show the teeth. Some kids will be like, "Wow! Those are sharp! So cool! I wonder what that wolverine would do to a rabbit..." Others will just be, "AHHH! Run away! Don't ever make me go near that thing ever again!"
These kinds of problems really separate those who end up loving math from those who do not. I present one or a dozen of these throughout the school year to my various math classes. Some of the kids LOVE it and try to figure out why it is and will read up on it when they go home and have all sorts of questions and really work to pay attention to the "proof." Others will just throw their hands up and say, "See! This is why I hate math!"
Basically, it polarizes the classroom. Those who enjoy thinking this way will get excited and encouraged to find out more. Those who already hate it will have fodder for their fears.
So, I guess what I'm asking here is: Is it a good idea to put forth these "paradoxical" problems in class?
Friday, August 13, 2010
Calculus Questionnaire
I gave a questionnaire to my calculus courses (one section of honors calculus, one of AP calculus AB, one of AP calculus BC) to get their minds going and preview some of the things we're doing. Below are the questions and why I asked them as well as any interesting answers given.
1. What is the furthest you've been away from home?
2.What is the largest number you can write in the space below?
3. What is the least probable (but still possible) event that you can think of? If you had to give it a percent chance of happening, what would it be?
4. What is the number right before 4?
5. Have you taken or are you taking physics?
6. Do you know the difference between the meaning of the words "velocity" and "speed?" What about "displacement" and "distance traveled?"
7. Using algebra skills, can you turn this:^3+8}{x}) into this:
into this: 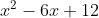
8. Using precalculus knowledge, write an equivalent expression for each of the following using trig identities you learned:
9. In as many steps as possible, explain how to make a bowl of cereal.
10. Find the shaded area of the shape in the picture below (Picture of a polygon that is a rectangle with triangles sticking out of each side.)
11. Find the following:
12. What do you think calculus is?
13. Write the word "minimum" below in cursive.
14. Haha! Wasn't that fun? Now, why are you taking this class?
Overall, I think it was a fun experience for them. It was interesting to note the difference in answers from the "creative" people from the "beaten-down-by-the-system" people. A couple kids in my BC class said, "You're going to hate me when you read my answers, Mr. P." When I asked why, they'd say, "Well, like for the 'biggest number' question, I just wrote a huge number 2." I tried not to smile too big.
1. What is the furthest you've been away from home?
- Why I asked: On a personal level, I wanted to know where some of my students have been. On a mathematical level, I wanted them to think about practical distances and how we measure distance. (Nobody said it, but I mentioned things like, "If you step out your front door, that might be the furthest away if you measure around the earth the other way. But why stop at measuring around the earth? Why not measure around the sun?")
- Interesting answers: Rural China, Ethiopia, Alaska, Australia, India
2.What is the largest number you can write in the space below?
- Why I asked: Getting at the concept of infinity, but I wanted to point out that infinity is not a number (at least not in the calculus we're doing). Creative answers would've also been good like a large-font 8 or something.
- Interesting answers: ZERO (written in tall letters), "a really big number," 9^9^9^9^9, infinity, "I'm not playing this game"
3. What is the least probable (but still possible) event that you can think of? If you had to give it a percent chance of happening, what would it be?
- Why I asked: Getting at the concept of limits, specifically as x approaches 0 from the right. Also interesting to see creativity and interests.
- Interesting answers: scoring an 18 on a professional golf course, being slapped by a walrus, gingers ever being cool, a squirrel causing a 30 car pileup, someone dying because they wore a black vest and choked on the buttons (what?), failing this class (yeah!), meeting everyone in the world, everyone getting along (:(), walking through a wall because your atoms pass through the spaces and reconfiguring on the other side
4. What is the number right before 4?
- Why I asked: Another attempt to get at limits. Also pointing out that 3.9999...(repeating) is not the answer because it actually is 4 (we'll learn later in the series section). I expected a lot of them to put 3 or 3.9(repeating). Maybe "4" because on the paper it's the previous number before the "4" from the end of the question.
- Interesting answers: 3, 3.9(repeating)
5. Have you taken or are you taking physics?
- Why I asked: It's not necessary for calculus, but our school doesn't offer calculus-based physics. So, those who have taken or are taking it can see some cool stuff like where the kinematics equations come from.
6. Do you know the difference between the meaning of the words "velocity" and "speed?" What about "displacement" and "distance traveled?"
- Why I asked: Straightforward. This may not be a necessary question in the future, but it gave me an opportunity to tell them one of the basic applications of calculus.
7. Using algebra skills, can you turn this:
- Why I asked: Practicing algebra using the difference quotient. We'll be coming up on these types of questions in the next week or so and I wanted to get a sense of where they were and give them an idea of what level of math we're looking at.
8. Using precalculus knowledge, write an equivalent expression for each of the following using trig identities you learned:
- Why I asked: For part (c) I expect them to put
I want them to have memorized these 3 IDs since it's easy to get most of the other ones we'll need from them.
9. In as many steps as possible, explain how to make a bowl of cereal.
- Why I asked: I thought it would be interesting mathematically to talk about how many steps we have to show at this level (eg If you have a quadratic, can you just write the answer on the next line or do you have to show the quadratic formula and all that?). I also wanted to talk about how mathematicians think in details. How far back would you go? (Go to the store to buy cereal? Grow wheat to make the cereal? Evolve plants to make the wheat? etc.) And what level of detail would you go into? (Send a signal from your brain to your arm muscle to extend your arm towards the spoon.)
- Interesting answers: Really, there are too many to list here, but one kid wrote more than 80 steps. Another had some sort of story in his where you go to the store to choose your cereal and then a few steps about trying pickup lines on the checkout girl.
10. Find the shaded area of the shape in the picture below (Picture of a polygon that is a rectangle with triangles sticking out of each side.)
- Why I asked: I wanted them to get started on thinking about integral calculus where we take a region and find its area by dividing it into smaller regions. Also, in broader terms, just taking a large problem and breaking it down into smaller, more manageable parts (see Sam's motto "turn what you don't know into what you do know").
11. Find the following:
- The slope of a line passing through the points (-1,2) and (3,-1).
- An equation of the line that goes through the points (2,4) and (5,2).
- An equation of a line with slope 0.
- Something in the school that has a positive slope
- Why I asked: Basic review. I also pointed out that the last part can be tricky, because if you go to the other side of the "up staircase," then it's a "down staircase" and has negative slope.
- Interesting answers: Knowledge gained, age of a student
12. What do you think calculus is?
- Why I asked: I thought it'd be interesting to know how many students actually knew what they were getting into. (Very few did.)
- Interesting answers: A difficult class that can only be understood when taught, the next class after precalculus, something to do with curves, I have no idea, hard math, the highest math class
13. Write the word "minimum" below in cursive.
- Why I asked: I always thought it was a fun word to write. You kinda scribble up and down a lot and then go back and dot some i's.
14. Haha! Wasn't that fun? Now, why are you taking this class?
- Why I asked: I thought it would be interesting to read the different reasons they thought of--especially in light of #12 on this questionnaire.
- Interesting answers: because it looks good on college apps, because it's next after precal, I wanted to take a math my senior year and I don't like statistics, I like punishing myself with challenging math classes, good question
Overall, I think it was a fun experience for them. It was interesting to note the difference in answers from the "creative" people from the "beaten-down-by-the-system" people. A couple kids in my BC class said, "You're going to hate me when you read my answers, Mr. P." When I asked why, they'd say, "Well, like for the 'biggest number' question, I just wrote a huge number 2." I tried not to smile too big.
Monday, August 9, 2010
SBG: Tiger Woods
I wouldn't necessarily call myself a sports fanatic, but I do have a few teams that I follow and I usually listen to sports radio on my 45 minute drive to school each morning. This morning, the topic of discussion (at least for the part where I was driving) centered mostly on Tiger Woods and his current streak of poor play.
For those of you who don't follow golf, basically, you know Tiger Woods was a pretty awesome golfer. Then there was a bit of scandal about his personal life and he took a long break from the sport. He is working his way back into playing tournaments now, but has been nowhere near his previous level on the course. While there have been "glimpses of his former self" on certain holes, the general consensus is that he is not only playing poorly, but his body language seems to sometimes say that he doesn't even want to be there anymore. This is especially distressing for Tiger Woods because one of his best features previously was his mental focus and toughness.
Anyhow, here's why I'm writing about it here. For those of you with experience in Standards Based Grading (or some other similar system where current knowledge is more heavily weighted than previous), how would this sort of situation play out in your classroom? By the way the PGA ranks its players, Tiger Woods is still the #1 golfer (even after his long absence and recent poor play--that's how dominant he was previously), but anyone watching his current performances would know that he doesn't deserve that title currently.
I guess I'm asking it in two parts. One, do we take into account that his poor performance may be largely due to personal issues from off the course? If so, how can we help the student (and our gradebook) separate those issues from the performances? And if we don't do any sort of "averaging" system with the numerical grades, what's the best way to assess this student?
Two, if we disregard the personal issues (or don't believe they're the cause), what do you do with a student who has performed exceptionally for such a long time and then drops off dramatically (maybe "senioritis" or some other non-catastrophic issue comes into play)?
For those of you who don't follow golf, basically, you know Tiger Woods was a pretty awesome golfer. Then there was a bit of scandal about his personal life and he took a long break from the sport. He is working his way back into playing tournaments now, but has been nowhere near his previous level on the course. While there have been "glimpses of his former self" on certain holes, the general consensus is that he is not only playing poorly, but his body language seems to sometimes say that he doesn't even want to be there anymore. This is especially distressing for Tiger Woods because one of his best features previously was his mental focus and toughness.
Anyhow, here's why I'm writing about it here. For those of you with experience in Standards Based Grading (or some other similar system where current knowledge is more heavily weighted than previous), how would this sort of situation play out in your classroom? By the way the PGA ranks its players, Tiger Woods is still the #1 golfer (even after his long absence and recent poor play--that's how dominant he was previously), but anyone watching his current performances would know that he doesn't deserve that title currently.
I guess I'm asking it in two parts. One, do we take into account that his poor performance may be largely due to personal issues from off the course? If so, how can we help the student (and our gradebook) separate those issues from the performances? And if we don't do any sort of "averaging" system with the numerical grades, what's the best way to assess this student?
Two, if we disregard the personal issues (or don't believe they're the cause), what do you do with a student who has performed exceptionally for such a long time and then drops off dramatically (maybe "senioritis" or some other non-catastrophic issue comes into play)?
Thursday, August 5, 2010
Experimental Classroom
I have an ideal situation with my Honors Calculus course for experimenting in the classroom. In Tennessee, there are basically 3 standards: Derivatives, Integrals, Applications. They are very vague, so I tend to just follow the AP Calculus AB curriculum and go at a slightly slower pace or less in depth. In addition, most students in Honors Calc are seniors, so it's pretty much a capstone course--they don't get college credit, so they'll have to take calculus again at college and I don't have to prepare them for another math course in high school either. So, I get a lot of leeway on what direction the class goes.
Just to keep my head above water (I've had 5 preps every year I've been teaching), I've not really taken advantage of the above very much. I've had the class follow behind the AB course and adjusted on the fly. Now that I feel more comfortable with the other courses I'm teaching, I'll be able to try some new/different things in there and move them into the other courses I teach if they work.
The two things I think I'd like to try at some point are: "Flipping the classroom" (record lectures and put them online for students to watch as homework, then in class work through the problem solving together) and "Standards-Based Grading" (tying assessment questions to specific skills and reporting student achievement based on level of mastery of each standard).
Since there are many blogs about SBG out there, I thought I'd try flipping the classroom and report my experiences of it, but the tech limitations (as mentioned in a previous blog entry) in our system are making me wonder if I can get it done. Among other things, youtube is blocked at our school. They do give us some web space to use, but they complain when you put too many files on there and it takes up too much memory. We're not really "allowed" to use outside resources. So, I could skirt the system and upload to youtube from my house and have the students watch the videos from home as well, but it would be going against the board policy.
I'll keep things updated here if/when I think I'm doing something interesting.
Just to keep my head above water (I've had 5 preps every year I've been teaching), I've not really taken advantage of the above very much. I've had the class follow behind the AB course and adjusted on the fly. Now that I feel more comfortable with the other courses I'm teaching, I'll be able to try some new/different things in there and move them into the other courses I teach if they work.
The two things I think I'd like to try at some point are: "Flipping the classroom" (record lectures and put them online for students to watch as homework, then in class work through the problem solving together) and "Standards-Based Grading" (tying assessment questions to specific skills and reporting student achievement based on level of mastery of each standard).
Since there are many blogs about SBG out there, I thought I'd try flipping the classroom and report my experiences of it, but the tech limitations (as mentioned in a previous blog entry) in our system are making me wonder if I can get it done. Among other things, youtube is blocked at our school. They do give us some web space to use, but they complain when you put too many files on there and it takes up too much memory. We're not really "allowed" to use outside resources. So, I could skirt the system and upload to youtube from my house and have the students watch the videos from home as well, but it would be going against the board policy.
I'll keep things updated here if/when I think I'm doing something interesting.
Hipster Teacher

Not me
You know how hipsters really like the indie band that nobody's ever heard of? Good or not, an unknown band will beat out a famous artist any day. Then they complain when that band gets famous or "sells out" by having songs featured on TV shows or movies or whatever. At least they can still say, "I knew them before..."
Part of me feels that way with you guys (anyone reading this). I get a lot out of discussing teaching, math, and everything else through blog comments and twitter and everything else. I get why I should share my experiences here with my companion teachers (although I don't think many of them would actually do it), but then the hipster in me comes out and I don't want to give up my trade-secrets!
Maybe one day I'll get around to giving a professional-development talk to the teachers in my area about the usefulness of a PLN and the online component of that, but in the meantime, I'm enjoying the spoils for myself!
Sunday, August 1, 2010
My New Blog (About Me)
For those who don't know me well yet, I'm sure you'll come to learn a few things about me as this goes on. Here are a few things to get you started:
As a blog, I'm not too interested in building up numbers of followers or becoming popular. I plan on just throwing idea-noodles out there and if something sticks to you, it's ready. Good luck finding something useful!
I'm a dog person.
I'm a math teacher in middle Tennessee at a public school in a suburb of Nashville. I have all the calculus courses offered at our school (Honors Calculus, AP Calc AB, and AP Calc BC) and then usually a couple extra courses to round out my schedule (in the past, Algebra II, but PreCalculus this coming year).
I think of myself as a "helper." That's partly why I'm only now starting this blog, but am somewhat well known in certain circles for my comments on others' blogs. If you look through my twitter feed, I bet you'll find that most of them are responses to others. It's also why I've become a teacher.
I am somewhat of a wolverine wrangler. I find myself mentally correcting grammar/spelling mistakes I see online (and elsewhere) all the time, I have trouble with "real world" problems because it gets really complicated really fast and I get overwhelmed very quickly, I love math because you can set the rules however you want and then go nuts within those boundaries while safely knowing the boundaries are there (later blog post on this maybe?).
The 2010-11 school year will start my experience at 4.5 years. I left graduate school (seeking a PhD in math at Vanderbilt) mid-year because it wasn't getting me where I wanted to go and I didn't really need it to teach high school math like I actually wanted. So, I took a position at an inner-city school in Memphis for the spring semester before making my way back to Nashville and starting at a new school that had just opened and have been there since.
The school where I am now opened in 2004 with just freshmen and sophomores and added a new class each year until 2006 when I showed up to teach their first calculus classes.
The good: Being a new school, the facilities are pretty great. The area for the school is mostly made up of students whose parents work at the auto plants nearby (formerly Saturn, now Nissan) and these parents tend to value education and keep an eye on their child's progress. Being in the rural South, most of our students are very polite and respectful. The Williamson County School District is one of the best in the state.
The bad: During the 6 years that the school has been open, there have been at least 3 instances of teachers and students having inappropriate relationships. This has led to severe limitations on our tech access (many sites are blocked at school for both teachers and students including youtube, google image searches, twitter, and many other useful sites). At this school more than most others I've seen, "senioritis" is a huge issue. Being in the rural South, there is a small amount of racism that persists in our school culture--two years ago we had to ban all students from wearing the "rebel flag" after some students found a noose in a kid's pick-up truck in the parking lot.
I'm sure you'll pick up quite a bit more about me and my teaching philosophy and whatnot as I let more of myself out through this blog (and comments on others').
Both of my parents are teachers (dad teaches Chemistry at a university; mom used to teach English and History on the middle school level until she moved into the library), so it's something I've grown up with and I owe them a lot for my getting this far.
As a blog, I'm not too interested in building up numbers of followers or becoming popular. I plan on just throwing idea-noodles out there and if something sticks to you, it's ready. Good luck finding something useful!
I'm a dog person.
Teaching Method: Dissonance/Randomness
One way that can really connect with students is adding a bit of "randomness" to the classroom. Especially in the math classroom where things are often kept very logical and dry, adding something different or even weird can make it memorable.
Discuss something in a funny accent (real or imagined).
Make up a word or name for a topic.
If your school dress code allows it, wear something crazy.
Ask students what they remember best from their previous math class and I bet it's something more along the lines of, "That time Jimmy fell out of his chair" or "When we sang that song" rather than some topic they were actually meant to learn.
Think back through your own past and the things that jump out at you were probably a little bit "off." But, this is especially true in today's culture. Consider the following cartoon that many of my students love:
It's just random enough to be funny. There are probably a few lines in there that stick out at you because they are just odd enough to make you laugh out loud.
Anyhow, in the classroom it doesn't have to be quite that odd, but something out of the ordinary can make something memorable. Here are some things I've done to make things stand out:
Zis ees za unit circle. YOU VILL LEARN EET!
The answer is 45 degrees, or as I call it 'Jimmy Blue Eyes.' (Remember--it doesn't have to make sense.)
Anything to mix it up a little and make it memorable!
Subscribe to:
Comments (Atom)