This post is inspired by a tweet from David Cox referring to a project one of his students must've been presenting: http://twitter.com/#!/dcox21/status/50600806541561856
As a math teacher, I get a lot of students who have learned math algorithmically. Even my "best" students in calculus often come in knowing how to do the work, but can't go much deeper than that. I think that's because math is often taught that way.
Sometimes I feel that way, too. I start to think, "If they can't understand the deeper meanings behind the subject, the least I can get them to do is follow a set of instructions to pass the high-stakes test at the end of the year." The problem is, many students can't even do that. So, I get frustrated that I laid out the 5 steps to factoring a trinomial and they still can't do it.
The point is, students see math as something coming down from the mountain on stone tablets. Reasons for either loving or hating math include: "There is only one correct answer to every problem" and "All you have to do is follow the steps and it works out."

Ahhh! Math!
Almost never have I been asked "Why?" in my math classes (other than "why are we doing this?").
As a kid I was the same way, but I was that way about most things. It never occurred to me to ask why the painter put a tree here and not there in his landscape; that must've been just the way it looked. I never thought to ask why the author used this word choice over another because that's just how you say something. Similarly in math class, I never thought to ask why our numbers look the way they do (why does the symbol 10 come after the symbol 9?) or why positives are on the right of the number line or why y's go over x's for slope. I was a good kid. I followed the rules. Someone older (and thus much wiser, of course) told me that's how it was and I took that to mean That's How It Is(TM).
But, did you know that math is completely man-made in the same way as the painting or novel? One plus one means absolutely nothing. Someone could've made a system where one plus one equals five and made up any rules they wanted. Logically, there's no real reason that the positives are on the right and up and negatives are on the left and down on the xy-plane. In fact, that's an arbitrary choice that the rest of the math doesn't even care about.
This was a great revelation to me when I finally "got it" in college (as a math major). We make it up.
Now, like any good system that sticks around, there has to be something in it that resonates with something else. Why have we all seen the Mona Lisa, but only a few people have seen your finger-painting from when you were 4? Because there's something common and interesting about Mona Lisa that resonates with a large audience. Your finger painting only meant something to you and your family, so they are the only ones who kept it in memory. Similar with these math choices (or my understanding of how evolution works). You can try anything you want, but only some things will stick because they are interesting or useful enough to propagate the species.

Bodies are an adult construct
Sure, the positive part of the x-axis could go to the left. But why? Since it's an arbitrary choice, why not go with our psychological convention that positive goes right. Then, when we need a new axis to represent a distinct direction, it seems to make the most sense to draw it vertically and have the positive part point up. Visually and even emotionally it feels right to do that.
So, why do we have the slope formula the way we do? Well, it makes sense to me that things like y = x that "go up" when you read from left to right should have a positive slope. Psychologically a graph that "increases" is a "good thing" and thus "positive." Now, how should we compare the graphs of y = x versus the graph of y = 2x? Well, the second one goes up faster, so it makes sense to me that it should be "more positive" so the slope should be a bigger number. With delta-y/delta-x you get 1 for the first and 2 for the second. With delta-x/delta-y you get 1 for the first again, but 1/2 for the second. Since math is somewhat arbitrary and we can make up whatever we want, I'm going to pick the first formula.
Sometimes these types of conventions lead to weird things. Math is full of some of these non-intuitive paradoxes. They're cool and interesting, but when presented out of context, students just lump them in with another crazy thing the teacher is asking us to believe. But what makes them cool and interesting is that they result from other conventions we have made because they made so much sense.
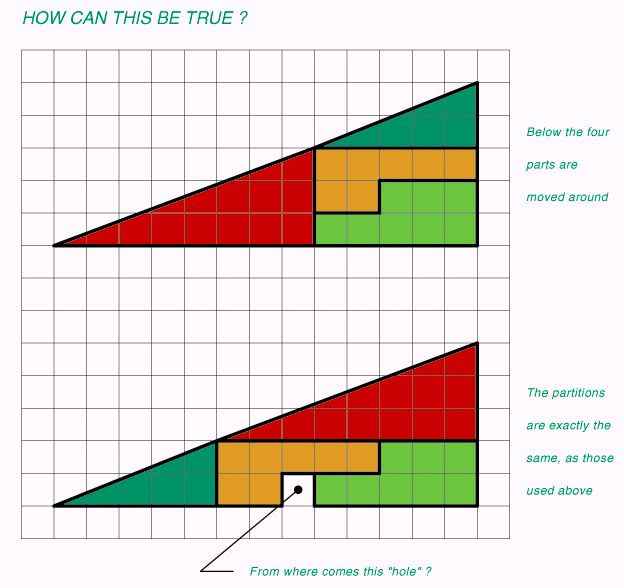
From where comes the hole!?!
For example: We go with the convention that right/up is positive and left/down is negative and we come up with the slope formula as above because it makes the most sense to do that. Well, what happens when you get a vertical line? Did it come from tilting your line more and more positive so that it is "the most positive you could ever get?" Or did it come from tilting your line the other way and making it more and more negative until it is "the most negative you could ever get?" From our basic understanding of positives and negatives these concepts are the two most opposite items we could think of with numbers, but here it stands visually as the same thing! At this point, we have two options. Accept the craziness of infinity and negative infinity and allow for weird things like that to happen OR redefine how we compute slope. Are we willing to come up with a more complicated way of computing a slope number that might resolve the infinity issue? Is there even a way to do that? It's an interesting conundrum.
There usually is a reason why math exists the way it does. Most of the math we teach in school has been around for hundreds, if not thousands, of years. It has resonated with people throughout cultures and time. But, at its root, the reason 1 + 1 = 2 is as deep as why the color red is more passionate than the color green.